Créer un réseau de neurones comportant plusieurs couches de profondeur et des milliers de neurones peut se faire de manière très simple grâce à des librairies comme Keras. Néanmoins, si vous souhaitez comprendre ce que vous faites, apprendre a implémenter un seul neurone soit même est une bonne idée.

Nous allons voir dans cet article comment le faire en python. Vous pouvez retrouver l’ensemble du code et les données d’entrainement dans ce repository github.

Préparation des données

Quand on fait du machine-learning, en général, c’est que l’on veut prédire quelque chose. Et comme cet article se veut le plus simple possible, j’ai construis un jeu de données à partir d’une liste de prénom trouvée ici auquel j’ai ajouté une valeur à prédire en fonction d’une règle très simple.

Le jeu de donnée contient une liste de prénom et une target à prédire que j’ai codé avec une petite règle qui renvoit “goodBoy” ou “badBoy” en fonction des lettres trouvées à une position donnée. Par exemple, si la 1ère lettre est un C, renvoyer goodBoy sinon si la 3ème lettre est un h renvoyer goodBoy etc…

Mon fichier d’entrainement training_data.csv est un csv contenant deux valeurs par ligne :

le prénom sur lequel nous allons faire une prédiction
le label goodboy ou badboy que notre neurone va devoir apprendre à prédire

Nous allons tout d’abord lire nos données puis les préparer pour pouvoir les faire rentrer dans notre neurone. En python ça donne :

from csv import reader

training_data = list()
with open('training_data.csv', 'r') as file:
    csv_reader = reader(file)
    for row in csv_reader:
        training_data.append(row)

print("training samples : {}".format(len(training_data)))

training samples : 7499

training_data[0]

['Claud', 'badBoy']

Ok, on a une liste training_data contenant 7499 données d’entrainement étant elles même des listes composées d’un prénom et d’une target à prédire.

Par contre, un neurone, ça prend des données en entrée, ça fait des calculs et le résultat obtenu nous permet de faire des prédictions. Notre donnée d’entrée est pour l’instant un prénom. On va donc ici limiter le nombre de caractères à 5, transformer ces caractères en une liste de float correspondant à leur index ascii. On va également en profiter pour modifier la target afin qu’elle vaille 1 pour goodBoy et 0 pour badBoy.

def transformName(name) :
    values = []
    for x in name.lower() :
        values.append(float( (ord(x))  ))
    return values

print(transformName("laurent"))

[0.44, 0.0, 0.8, 0.68, 0.16, 0.52, 0.76]

def transformTarget(target) :
    if target == "goodBoy" :
        formatedTarget = 1.0
    else :
        formatedTarget = 0.0
    return formatedTarget

print(transformTarget("badBoy"))

0.0

formatedDataset = []
for name,target in training_data :
    values = transformName(name)
    target = transformTarget(target)
    formatedDataset.append([values,target])

print("prénom en nombre : {}".format(formatedDataset[0][0]))
print("target en nombre : {}".format(formatedDataset[0][1]))

prénom en nombre : [99.0, 108.0, 97.0, 117.0, 100.0]
target en nombre : 0.0

formatedDataset[0:3]

[[[99.0, 108.0, 97.0, 117.0, 100.0], 0.0],
 [[97.0, 108.0, 112.0, 104.0, 111.0], 1.0],
 [[99.0, 104.0, 114.0, 105.0, 115.0], 0.0]]

Calcul de l’output du neurone

Bien. On a maintenant nos données prête à l’emploi. Il va falloir maintenant être capable de calculer une valeur pour notre neurone et se servir de celle ci pour réaliser une prédiction.

Chaque donnée d’entrée (elles sont ici au nombre de 5), est liée à notre neurone par un poid. Voici un schéma permettant de mieux visualiser l’ensemble des paramètres :

alt text

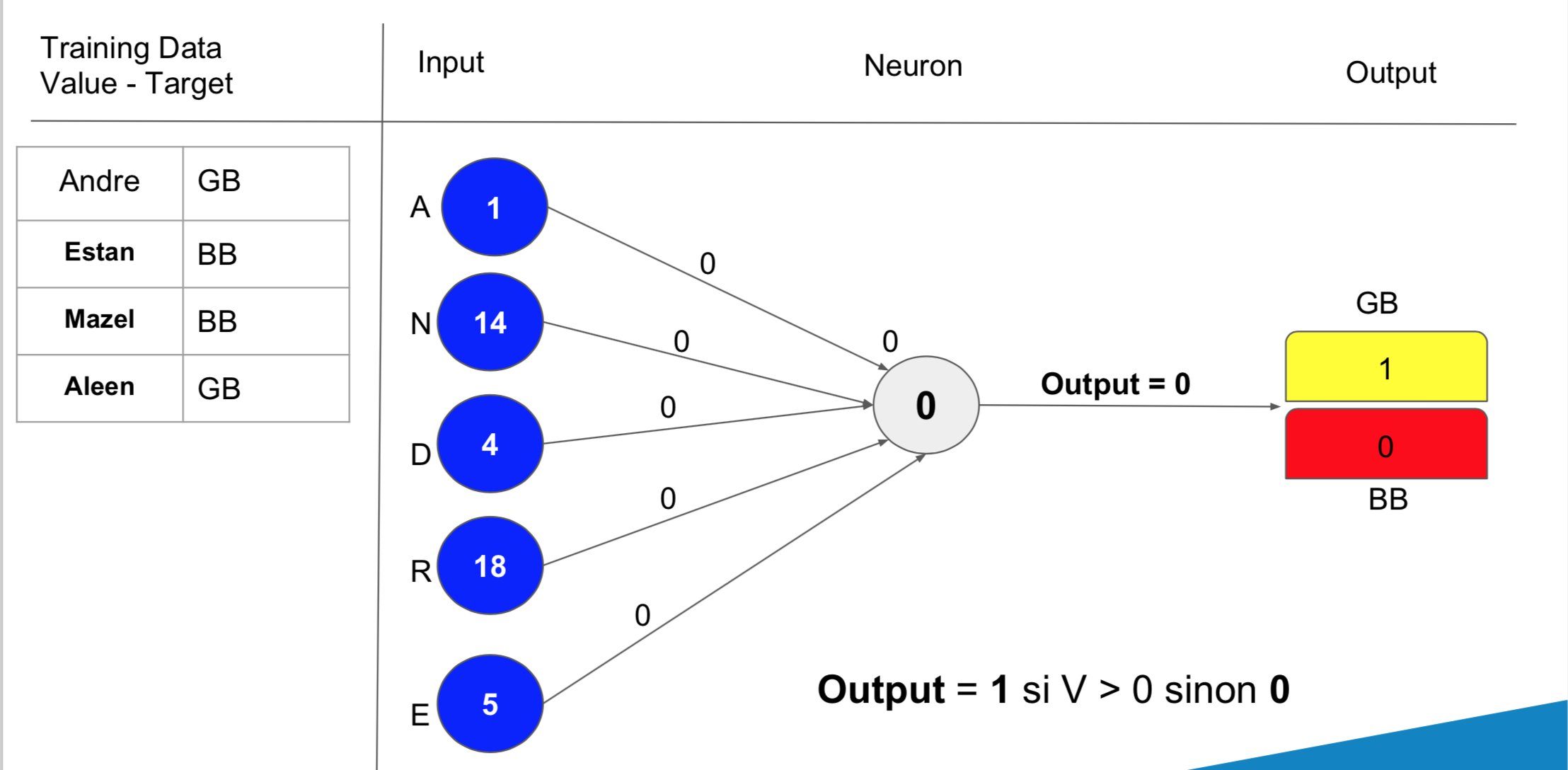
La valeur d’un neurone pour une entrée donnée correspond a la somme pondérée des entrées multipliées par leurs poids respectif auquel on ajoute le biais du neurone. Cette valeur calculée va nous permettre de déduire l’output du neurone. La déduction est simple, l’output vaut 1 (goodBoy) si la valeur V calculée est strictement supérieur à 0. Elle prend 0 pour badBoy dans le cas contraire.

Voici ci-dessous la fonction calcul_output qui permet de calculer la valeur V de notre neurone pour un prénom donné et de renvoyer l’output déduite :

def cacul_output(row, poids, biais):
    V = 0.0
    for i in range(5):
        V += row[i] * poids[i]
    V =+ biais
    if V > 0:
        return 1.0
    else :
        return 0.0

Prédire -> mettre à jour

Nous allons maintenant faire des prédictions sur l’ensemble de nos données. Lors de chaque prédiction, nous allons mettre à jour nos poids et notre biais pour essayer de faire mieux la prochaine fois.

Je vais définir le nombre d’époques que nous allons réaliser à 10. C’est quoi une époque ? Excellente question ! Une époque correspond au moment où nous aurons présenté l’ensemble de nos données à notre neurone. A ce moment là, nous aurons mis à jour nos poids 7499 fois ! Et on ne va pas s’arrêter là. On va présenter l’ensemble de nos données 10 fois à notre neurone soit 10 époques.

La variable learning_rate est une constante permettant de mettre à jour nos poids et notre biais de façon plus ou moins “douce”. La mise à jour des poids et du biais se fait de la manière suivante :

alt text

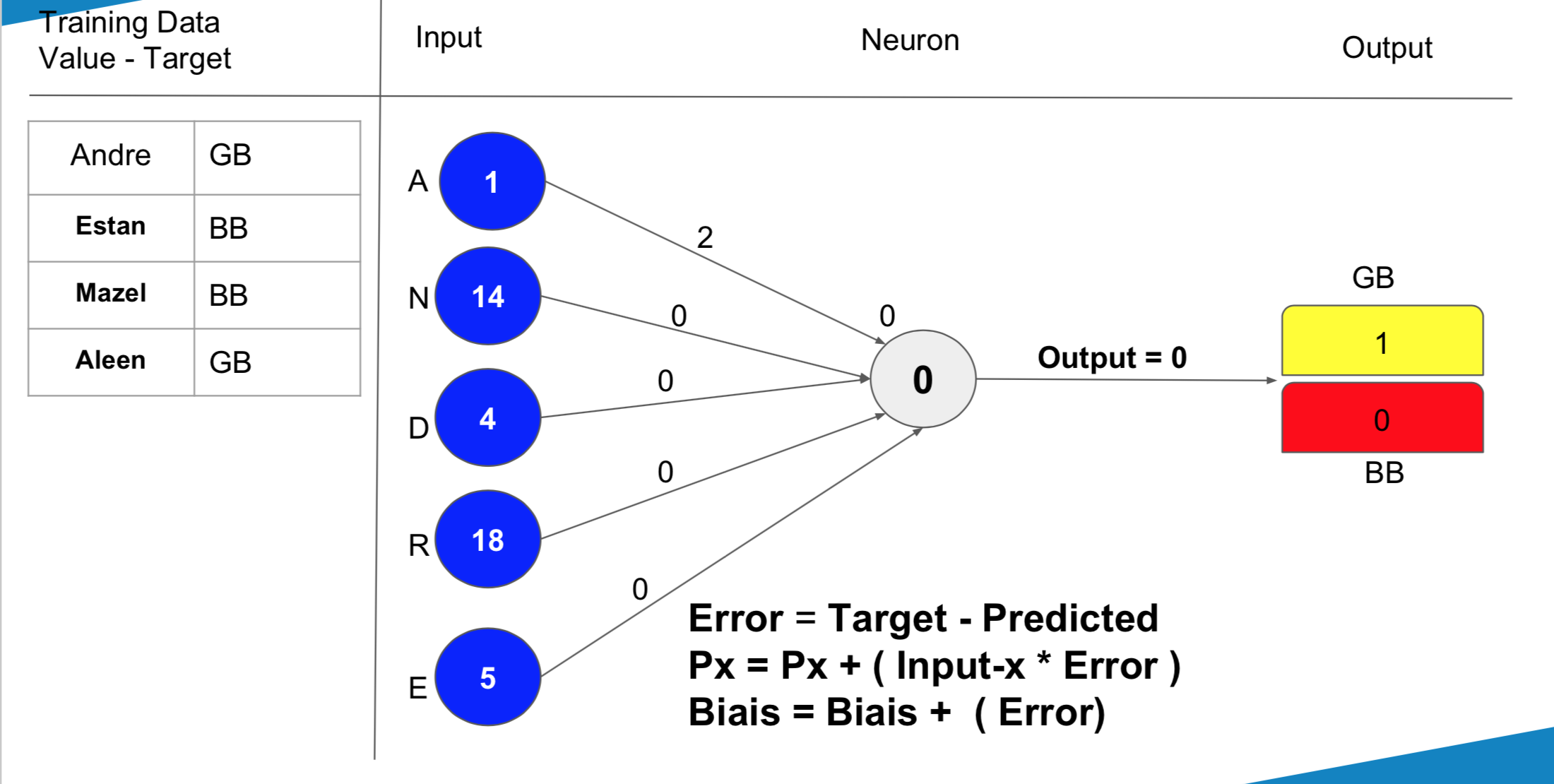
Voici ci-dessous le code correspondant à la mise à jour des poids ainsi que le code permettant de présenter l’ensemble de nos données 10 fois à notre neurone :

epoques=10
learning_rate=0.1

def updatePoidsEtBiais(row, poids, biais, error) :
    for i in range(5):
        poids[i] = poids[i] + row[i] * error * learning_rate
    biais = biais + error * learning_rate
    return poids, biais

def entrainement(dataset):
    biais = 0.0
    poids = [ 0.0, 0.0, 0.0, 0.0, 0.0 ]
    for epoque in range(epoques):
        goodPredictions = 0
        for row, target in dataset:
            Output = cacul_output(row, poids, biais)
            if target == Output :
                goodPredictions += 1
            error = target - Output
            poids, biais = updatePoidsEtBiais(row, poids, biais, error)
        print("taux de précision : {}".format(goodPredictions / 7499))
    return poids, biais

poids, biais = entrainement(formatedDataset)

taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505
taux de précision : 0.7322309641285505

On voit ici qu’une seule époque aurait suffit car le taux de précision n’augmente plus dès la fin de la 1ère époque. Nous avons à la fin une liste de poids et un biais :

poids

[-6786.000000000526,
 7778.999999999313,
 -1638.0000000000173,
 -927.9999999999776,
 -131.00000000000074]

biais

0.0

Ce qui est top, c’est qu’on peut maintenant donner ces poids et ce biais à quelqu’un pour qu’il puisse faire des predictions lui même grâce à la méthode calcul_output sans avoir besoin d’entrainer le neurone !

73% de précision c’est pas mal pour un truc codé from scratch :-) On va maintenant essayer d’utiliser notre méthode de prédiction sur de nouveaux prénoms.

Prédiction sur de nouvelles données

La fonction testPrediction ci-dessous prend un prénom en paramètre que l’on formate de la même façon que nous l’avons fait pour le jeu de donnée d’entrainement. On appele ensuite la méthode calcul_output avec nos poids et notre biais et on retourne la prédiction goodBoy quand on récupère la valeur 1 :

def testPrediction(name) :
    name = name + 'x' * (5 - len(name)) if len(name) < 5 else name
    nameFormated = [float((ord(x))) for x in name[0:5].lower()]
    result = cacul_output(nameFormated, poids, biais)
    return "goodBoy" if result == 1 else "badBoy"

testPrediction("Alex")

	goodBoy

22 neurones sur 4 couches !

Ça a de la gueule ça non ? :-) Nous n’allons pas recoder ça from scratch cette fois ci mais plutôt utiliser la librairie Keras. Vous allez voir que ça va être beaucoup plus simple…

Tout d’abord, on importe de quoi faire le boulot.

from keras.models import Sequential
from keras.layers.core import Dense
from sklearn.preprocessing import StandardScaler
import numpy as np

On peut maintenant définir l’architecture de notre réseau de neurones. Soit une couche de 12 neurones qui va recevoir 5 valeurs d’entrée. Suivi d’une couche de 6 neurones, une de 3 et un neurone final dont l’output sera la prédiction.

model = Sequential()
model.add(Dense(12, input_dim=5, kernel_initializer='normal', activation='relu'))
model.add(Dense(6, kernel_initializer='normal', activation='relu'))
model.add(Dense(3, kernel_initializer='normal', activation='relu'))
model.add(Dense(1, kernel_initializer='normal', activation='sigmoid'))

model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])

X est un array contenant l’ensemble de nos données à prédire, Y un array de même taille contenant les véritables réponses.

X = [ name for name, target in formatedDataset ]
X = np.array(X)
scaler = StandardScaler()
scaler.fit(X)
scaler.transform(X)

Y = [ target for name, target in formatedDataset ]

On peut maintenant entraîner notre réseau grâce à la méthode fit de Keras :

model.fit(np.array(X), Y, epochs=30, batch_size=5, verbose=1)

Epoch 1/30
7499/7499 [==============================] - 2s 238us/step - loss: 0.3588 - acc: 0.8410
Epoch 2/30
7499/7499 [==============================] - 2s 239us/step - loss: 0.3189 - acc: 0.8410
Epoch 3/30
7499/7499 [==============================] - 2s 238us/step - loss: 0.3056 - acc: 0.8410
Epoch 4/30
7499/7499 [==============================] - 2s 235us/step - loss: 0.2978 - acc: 0.8410
Epoch 5/30
7499/7499 [==============================] - 2s 235us/step - loss: 0.2943 - acc: 0.8410
Epoch 6/30
7499/7499 [==============================] - 2s 236us/step - loss: 0.2931 - acc: 0.8422
Epoch 7/30
7499/7499 [==============================] - 2s 238us/step - loss: 0.2926 - acc: 0.8550
Epoch 8/30
7499/7499 [==============================] - 2s 236us/step - loss: 0.2916 - acc: 0.8576
Epoch 9/30
7499/7499 [==============================] - 2s 237us/step - loss: 0.2916 - acc: 0.8557
Epoch 10/30
7499/7499 [==============================] - 2s 237us/step - loss: 0.2904 - acc: 0.8624
Epoch 11/30
7499/7499 [==============================] - 2s 237us/step - loss: 0.2896 - acc: 0.8660
Epoch 12/30
7499/7499 [==============================] - 2s 238us/step - loss: 0.2893 - acc: 0.8644
Epoch 13/30
7499/7499 [==============================] - 2s 248us/step - loss: 0.2889 - acc: 0.8661
Epoch 14/30
7499/7499 [==============================] - 2s 242us/step - loss: 0.2879 - acc: 0.8681
Epoch 15/30
7499/7499 [==============================] - 2s 239us/step - loss: 0.2872 - acc: 0.8673
Epoch 16/30
7499/7499 [==============================] - 2s 242us/step - loss: 0.2853 - acc: 0.8653
Epoch 17/30
7499/7499 [==============================] - 2s 246us/step - loss: 0.2845 - acc: 0.8618
Epoch 18/30
7499/7499 [==============================] - 2s 247us/step - loss: 0.2842 - acc: 0.8633
Epoch 19/30
7499/7499 [==============================] - 2s 247us/step - loss: 0.2823 - acc: 0.8608
Epoch 20/30
7499/7499 [==============================] - 2s 240us/step - loss: 0.2795 - acc: 0.8624
Epoch 21/30
7499/7499 [==============================] - 2s 240us/step - loss: 0.2739 - acc: 0.8633
Epoch 22/30
7499/7499 [==============================] - 2s 250us/step - loss: 0.2655 - acc: 0.8692
Epoch 23/30
7499/7499 [==============================] - 2s 247us/step - loss: 0.2524 - acc: 0.8775
Epoch 24/30
7499/7499 [==============================] - 2s 254us/step - loss: 0.2345 - acc: 0.8865
Epoch 25/30
7499/7499 [==============================] - 2s 252us/step - loss: 0.2148 - acc: 0.9085
Epoch 26/30
7499/7499 [==============================] - 2s 246us/step - loss: 0.1912 - acc: 0.9279
Epoch 27/30
7499/7499 [==============================] - 2s 241us/step - loss: 0.1661 - acc: 0.9473
Epoch 28/30
7499/7499 [==============================] - 2s 239us/step - loss: 0.1475 - acc: 0.9596
Epoch 29/30
7499/7499 [==============================] - 2s 245us/step - loss: 0.1348 - acc: 0.9631
Epoch 30/30
7499/7499 [==============================] - 2s 248us/step - loss: 0.1303 - acc: 0.9620

On arrive au bout de 30 époques à une précision de 96% ! C’est beaucoup mieux.

Et voici comment faire des prédictions avec notre réseau de neurones :

def testPrediction(name) :
    name = name + 'x' * (5 - len(name)) if len(name) < 5 else name
    nameFormated = [float((ord(x)-ord("a")) / (ord("z")-ord("a")) ) for x in name[0:5].lower()]
    npArray = np.array([nameFormated])
    scaler.transform(npArray)
    result = model.predict_classes(npArray)
    return "goodBoy" if result == 1 else "badBoy"

result = testPrediction("Alex")

Autopsie d'un neurone artificiel